(REFERENCE FROM: http://www.megamanual.com/PWC/LSU4.htm)
Before one can understand the PWC hardware circuitry and control software, it helps to understand how the wideband oxygen sensor [WBO2] operates (These sensors are also known as universal exhaust gas oxygen sensors [UEGO]).

The Precision Wideband Controller circuit is intended to be used to directly control the fuel mixture, so it needs to be accurate and repeatable. When tuning an engine on the road or on a dynamometer, it is desirable to have a means of monitoring engine air-fuel ratio (AFR), which can also be expressed in terms of lambda (λ). During these tuning sessions, engine/vehicle/environmental parameters are kept constant with the exception of the variable being tuned. Wideband meters use a user-interface to obtain the current AFR/lambda so that the engine tuner can adjust and optimize fuel delivery.
The Precision Wideband Controller is a mixture feedback device. A mixture feedback device is used to determine the instantaneous mixture of a running engine, where these parameters are introduced back into the fueling equation in the ECU for real time injector pulse width correction. The main demand of the mixture feedback device is that it needs to be repeatable over absolutely all environmental conditions the same readings for extreme hot or freezing cold conditions. This response is introduced back into the fueling equation in the ECU for real time injector pulse width correction. The main demand of the mixture feedback device is that it needs to be repeatable over absolutely all environmental conditions – the same readings for extreme hot or freezing cold conditions.
In addition, the response function of the wideband UEGO sensors is dependent on parameters like hydrocarbon type, operating temperature, exhaust temperature, exhaust back pressure, etc. If any of these parameters change, then the controller needs to know this and be able to correct/compensate.
Bruce and Al purchased a 5-gas Horiba meter directly from Horiba, so this along with the use of primary gas standards for test gases, lets them know exactly what the sensor sees.
There really is a difference between a wide band EGO meter and a wide band device which directly controls fuel mixture – the mixture device needs to be accurate at all times, or at least be able to notify the mixture control that the WB signal is not within tolerance. Heater control is very import. Steady state running is easy to monitor.
The problems come from events such as recovery after acceleration, where the temperature of the sensor will vary due to changes in exhaust flow. If the sensor temperature changes then the required pump current to maintain equilibrium changes as well (everything else remaining the same) – you either have to keep the sensor temperature regulated or have correction factors – or both (see section 5.1 of the LSU data sheet for a temperature graph with different engine operating conditions and the effect in exhaust temperature).
Throw in transient response for the pump loop, accuracy of the pump measurement circuitry itself, etc. and things can go wrong – and at the wrong time. Getting a handle on all of these effects (and their magnitude) is important for anything that is maintaining a AFR mixture. And the only way to get an handle is to compare against a known calibrated system and a lot of testing.
The wideband air/fuel ratio sensor combines an oxygen-sensing “Nernst” cell from the narrow band sensor with an “oxygen pump” to create a device that gives a wide range response to various air/fuel ratios. The Nernst cell senses exhaust gas oxygen in the same as a conventional narrow band O2 sensor. If there is a difference in oxygen levels across the ZrO2 sensor element, current flows from one side to the other and produces a voltage.
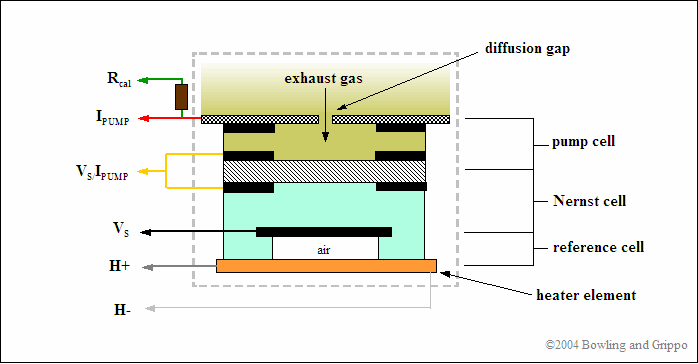
The wideband exhaust gas oxygen sensor comes in many constructional forms, but are basically similar in nature. They consist of two parts: a Nernst reference cell and an oxygen pump cell, co-existing in a package that contains a reference chamber and heater element (used to regulate the temperature of the Nernst/pump).
Before delving deeply in the operation of the Nernst and pump cells, it is important to understand what the sensor is actually trying to measure. To start, lets understand the chemical reactions due to combustion.
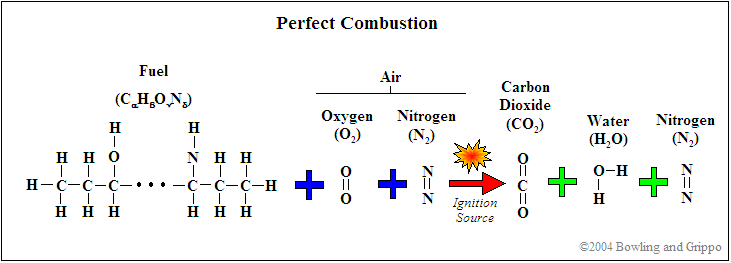
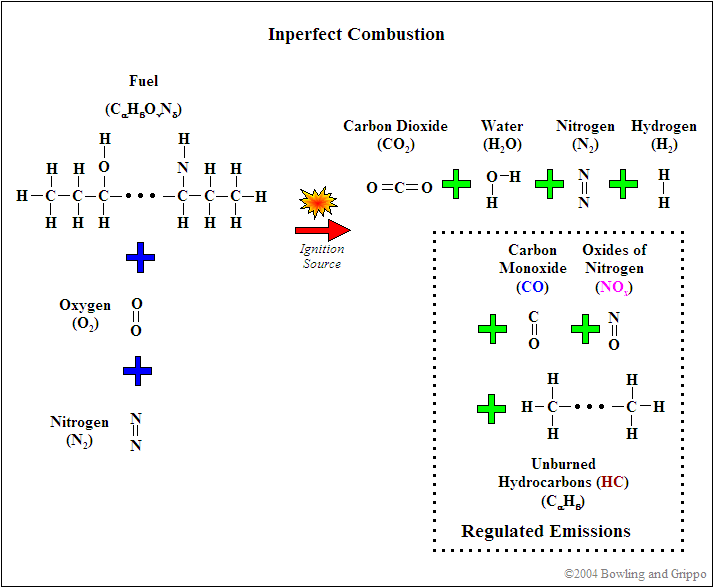
First, realize that for combustion to occur, there needs to be fuel (such as hydrocarbon) and a source of oxygenates (i.e. oxygen and/or molecules or partial molecules which contain oxygen). In addition, there are diluents which are present in the mixture but do not contribute to the actual combustion (for example, nitrogen [N2]). This holds true for any combustion event, whether inside of an internal combustion engine or a small campfire.
Second, every atom is conserved in the combustion process, so it is possible to use exhaust gas constituents to reconstruct the amount of fuel and oxygenates before combustion. If this was not the case, then wideband oxygen sensors would not be capable of determining pre-combustion air/fuel ratio.
It is possible to express the combustion event as a balance of input reactants: fuel, oxygenates, and diluents (for example gasoline mixed with air) to the resultant combustion products (i.e. the composition of exhaust gas). Note that this is a chemical balance, meaning that every element needs to be accounted for in its molecular balance, before and after the combustion event. In other words, if we know the proportions of fuel, oxygenates, and diluents entering the engine, one can determine the species composition in the exhaust gas. And we can work backwards. If we know the species in the exhaust we can determine the ratios of air and fuel (both in molar quantity and molecular mass).
Let us represent the chemical composition of the intake fuel as carbon, hydrogen, oxygen, and nitrogen, in proportion of:
Normally, chemists work with a quantity called a “mole”, which is a specific very large number of atoms or molecules of any given species [type]. Combining one mole of atom A, with two moles of atom B is the same as combining one atom of A with two atoms of B, many, many times over.
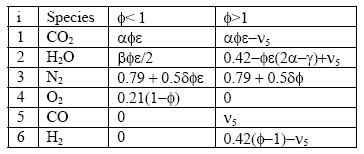
We can combine the fuel with air and write down a simple balance equation for combustion and balance for the molar quantities before and after combustion:
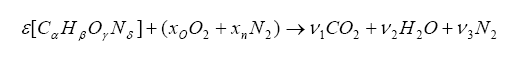
Note that we have more unknowns than equations, so we will have to use some known constraints to help us solve for the unknowns. For one, atoms are conserved (i.e. what goes in must come out), so we can immediately write the following relations (known as the element balance equations):
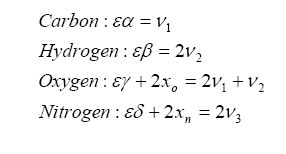
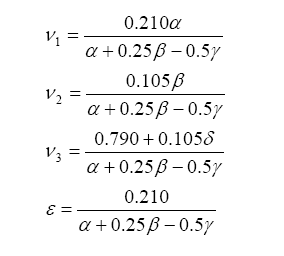
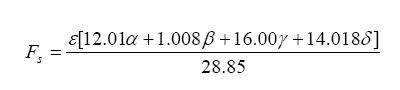
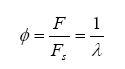
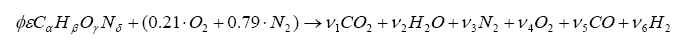
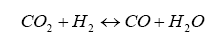
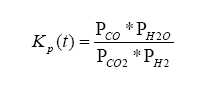
With this, ν5 can be evaluated as a solution to a quadratic:
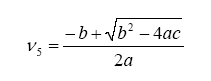
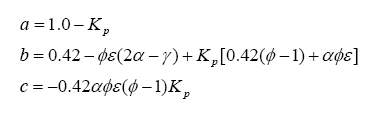
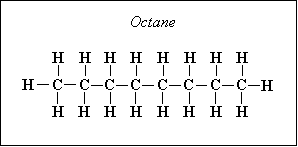
Next, one can divide the hydrocarbon/fuel expression by a constant, which will make the carbon subscript equal to one. This creates a H/C ratio, a O/C ratio, and a N/C ratio – these are often seen in the literature. For example, the fuel C8H18 (octane) can be normalized to become C1H2.25 = CH2.25, where the H/C ratio is 2.25, the O/C ratio is 0 (because there is no oxygen component) and N/C of 0 (no component), and, of course, the C subscript is 1. Another example is the fuel CH3NO2, which already has a C subscript of 1, so the H/C ratio is 3, the N/C ratio is 1 and the O/C ratio is 2. Just note that either form of expressing the fuel is identical.
Note: For those who are interested in experimenting with the above equations, we have developed the program COMBAL, a PC application running under Windows. One basically enters the H/C and O/C ratios, exhaust gas equilibrium, and the target lambda, and it generates the percent moles of each of the gas species. A comparison check using the Brettschneider equation is also performed. The application can be downloaded from:
Are you confused yet? If you are, do not be concerned. All we are outlining here is that with known input fuel, diluents, and oxygenates, one can predict the gas concentrations in the exhaust. And we can go backwards – with measured gas constituents it is possible to determine the input mixture in terms of either lambda or air/fuel ratio. Go back and re-read the section a few times, it is important to understand this aspect.
There is much more to the analysis not shown here – see the Bowling & Grippo paper on the entire analytical method for the Precision Wideband Controller for more info.
The Nernst cell and oxygen pump cell are wired together in such a way that it takes a certain amount of current to maintain a balanced oxygen level in the diffusion gap. Measuring this current flow allows the Precision Wideband Controller to determine the exact air/fuel ratio the engine is operating at.
The pump cell can either consume oxygen or consume hydrocarbon fuel in the pump cell cavity, depending on the direction of the pump cell current flow (Ipump).
In normal sensor operation, exhaust gas passes through the diffusion gap into the pump cell. That exhaust gas is often either rich or lean of stoichiometric. Either condition is sensed by the reference cell which produces a voltage (Vs) above or below the Vref signal, just like a narrow band sensor).
Combustion is rarely perfect though. Even with the correct air/fuel ratio (AFR), combustion can still be incomplete, and CO, H2, NOx, and hydrocarbons (HC) can form. This can be caused by quenching (of the flame front against the “cold” surfaces of the combustion chamber), crevice volumes (above the rings between the piston and cylinder), and many other factors.
When the air/fuel mixture is lean, the reference cell produces a low Vs (lower than 0.450 volts). The Precision Wideband Controller sends the pump current in the opposite direction to consume free oxygen. The pump cell requires a “positive” current that goes from zero up to 1.5 milliamps as the mixture becomes “free air”.
When the air/fuel mixture is 14.7:1 (the stoichiometric ratio for gasoline), the pump cell requires no output current. Since the free oxygen or free fuel has been neutralized by the pump current, the Vs feedback signal goes to about 0.450 volts (the same as the Vref value).
To sense a wide range of air/fuel ratios, the oxygen pump uses a heated cathode and anode to pull some oxygen from the exhaust into a “diffusion” gap between the two components. The pump is driven by two PWM or processor ports in opposite polarity (using either a H-bridge setup or direct processor port drive), and the Precision Wideband Controller measures the time when the reference cell passes through 0.45 volts. It can then adjust the PWM timing to bracket this 0.45 volt stoichiometric flipping point.
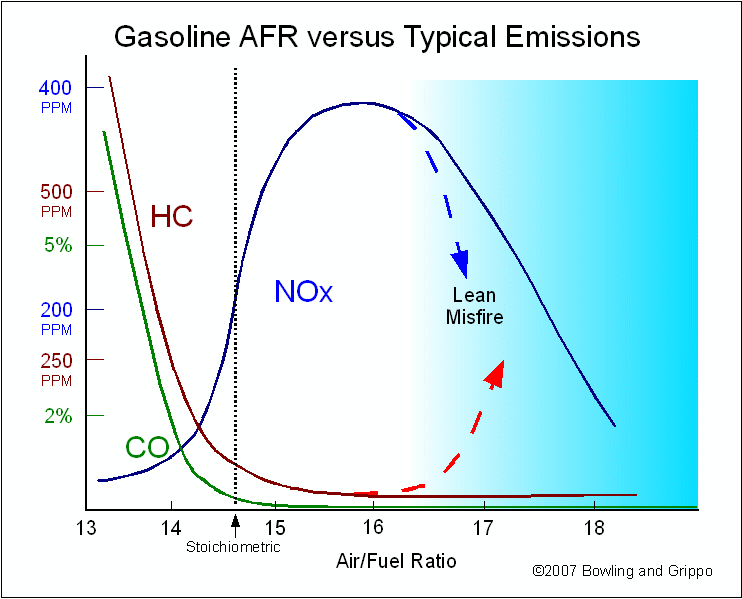
Like a conventional narrow band sensor, the Precision Wideband Controller circuit produces a low-voltage signal when the air/fuel ratio goes lean, and a high-voltage signal when the mixture is rich. But instead of switching abruptly at stoichiometric, it produces a proportional change in the voltage. It increases or decreases in proportion to the relative richness or leanness of the air/fuel ratio. With a stoichiometric air/fuel ratio of 14.7:1, the wide-band O2 sensor will produce a steady 0.450 volts. If the mixture goes a little richer or a little leaner, the sensor’s output voltage will only change a small amount instead of rising or dropping dramatically.
The result is a sensor element that can precisely measure air/fuel ratios (AFR) from very rich (10:1) to extremely lean (free air). This allows the Precision Wideband Controller to control the air/fuel ratio directly. Instead of switching the air/fuel ratio back and forth from rich to lean to create an average balanced mixture, the PWC can simply add or subtract fuel as needed to maintain a stoichiometric ratio of 14.7:1 or any other ratio.
Another difference between the narrow band sensor found in most automobiles and the wide band oxygen sensor is in the heater circuit. The heater power is closed loop controlled while the measurement is done, so that a nominal sensor internal resistance of Ri=80 Ohms (measured with 1 to 4 kHz) is reached, this corresponds to a sensor ceramic temperature of approx. 750°C when the sensor is new. The Precision Wideband Controller (PWC) heater circuit is modulated to maintain a consistent operating temperature of 1300°F to 1500°F (700°C to 800°C). The sensor takes about 20 seconds to reach operating temperature from a cold start.
The sensor incorporates a 10 Watt (3.2 ohms at 20°C, 2.1 ohms at -40°C) heater that ensures the sensors is kept at the nominal operating temperature of 750°C (~1400°F). The current to the heater is limited by the Precision Wideband Controller circuitry to prevent excessive heating during warm-up. The sensor heater must never be connected directly to battery voltage, it must always be controlled by the Precision Wideband Controller. Starting the sensor heating before engine start is not advisable, it will harm the sensor.
The maximum operating exhaust gas temperature for the sensor is up to 850°C (1560°F). If the maximum exhaust gas temperature is exceeded, the heater power must be switched off, and the accuracy of the sensor signal is reduced. Hot exhaust gas with a temperature above the operating temperature of the ceramic gives also a deviation of the ceramic temperature and the sensor output signal. Cold exhaust gas, in addition with high gas velocity, can lead to a reduced sensor ceramic temperature, if the heater control is not able to keep the constant ceramic temperature. This leads to a deviation of the sensor output signal. As a general rule, a temperature change of the sensor ceramic gives a deviation of the sensor output signal of:
At the electrodes, the following reactions occurs:
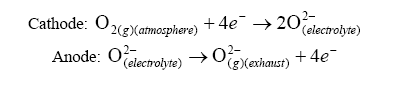
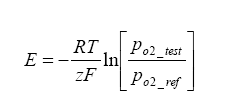
R is the Universal Gas Constant = 8.31 J*K-1*mol-1,
T is the temperature of the cell in Kelvin,
F is the Faraday Constant = 96500 Cmol-1,
Z is the electrons transported per O2 = 4.
Because there is a heater maintaining the Nernst cell at an elevated temperature, a temperature gradient exists which generates an offset voltage. We can add this term to the above term, and in the process we can also simplify the calculation by converting from base e to base 10 logarithms:
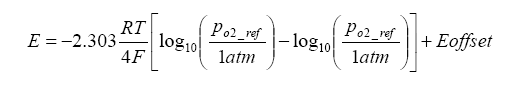
Continuing the discussion of the planar structure, there exists an internal “diffusion cavity” – this cavity is where the sample of exhaust gas is “trapped”, as well as where the Nernst and pump sections face. How does the gas get there? By a diffusion process, the exhaust gas to be sampled enters the cavity. Not to get too “geeky” about the diffusion process, but suffice to say that there are two diffusion mechanisms:
- one is known as molecular diffusion, and
- the second is known as Knudsen diffusion, or “fine-pore” diffusion.
It is very important to note: Knudsen diffusion is temperature dependent – this means that the porosity of the test chamber (i.e. how much gas can enter/exit) depends on the sensor head temperature – this is why pumping current (described next) is different for different temperatures, as well as exhaust back pressure dependence.
The aforementioned oxygen pump – this is what makes a run-of-the-mill oxygen sensor a true wideband unit – is really just another Nernst-type cell with an external current applied to it.
We talked about the “cavity” above where sample exhaust gas exists and on one side is the Nernst measurement cell. On the other side is the pump cell – this cell is used to transport oxygen into and out of the measurement cavity. In very simplistic terms, if the exhaust gas in the measurement cell is lean, then there is excess oxygen (lean mixtures mean excess oxygen). We can “turn on the pump” to remove oxygen from the reference cavity – and with the proper feedback monitoring of the Nernst measurement cell we can pump out just enough oxygen to achieve a stoichiometric balance (roughly when the Nernst measurement cell reads 0.45 volts or thereabouts).
The best part of all: if we monitor the pump current, we can use this to determine lambda (λ) and AFR Pump current is related to the amount of oxygen pumped out as a function of time as:
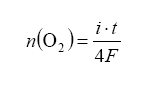
We have explained the excess-oxygen case where the air-fuel mixture is lean. How does it operate on the oxygen-depleted side, or rich air/fuel ratio side? For this case, oxygen is ‘pumped’ into the measurement cavity simply by reverse application of current on the pump element. Feedback on the Nernst measurement cell indicates when stoichiometric equilibrium has been achieved.
Now, something should be bothering your gut right about now…
The pump cell operates on oxygen ion transport, but we are in a situation where there is no oxygen in the air-fuel mixture (i.e. we are rich). If we become much more rich, we still do not have oxygen. Super rich, and still no oxygen. How can there be a feedback situation in this case?
It turns out that within the diffusion measurement cavity, the following chemical reactions are occurring:
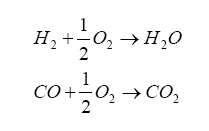
And it turns out that H2 and CO are present in significant amounts for a rich AFR, and can be related to lambda by the elemental balance equation for the fuel/oxygenates/diluents we derived above.
This is not exactly right, in that we are dealing with a gas balance and the pump is really an electrochemical cell (click on the links for background information on Le Châtelier’s Principle for equilibrium balance rules, as well as the Ideal Gas Law), so we need the oxygen in the H2O and CO2 as donors for the reaction – this where the pump gets its oxygen. It is a balance, and by changing the amount of current pumped into the pump we can change the balance. The balance is also driven by the water-gas reaction, discussed later on.
Finally, lambda (λ), what we all want to know, is related to all of the exhaust gas components in simplistic relation known as the Brettschneider equation:
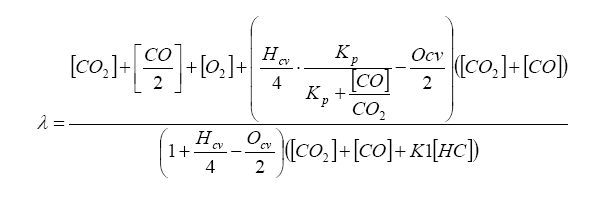
So, armed with all of this knowledge, we can write an equation relating pump current compared to exhaust gas component, then stick this into the Brettschneider equation (or a more advanced form – see the Bowling & Grippo paper). For the lean mixture side where there is excess oxygen, the pump current equation is:
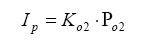
For the rich mixture side, where there is no oxygen, the sensor measures the amount of CO and H2 in the exhaust gas (partial pressure):
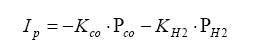
Also note that on the rich side, the UEGO sensor reacts to unburned hydrocarbons as well. However, in normal combustion, the amount of unburned hydrocarbons are in the parts per million region, whereas the moles of CO and H2 are substantially higher (like in the 10 – 20% range).
Measuring the Nernst Cell Resistance
Accurate temperature control of the wideband UEGO probe is an absolute requirement during operation. Changes in UEGO probe temperature will result in a change in required pump current (from the difference in diffusion in and out of the measurement cavity), so monitoring the temperature allow for corrections to be applied to the measurements. The wide band sesnor does not have any form of direct temperature measurement (i.e. thermistor,thermocouple, etc.).
However, monitoring the resistance of the reference cell yields a close representation of the probe temperature – the resistance of the reference cell varies with temperature. The Nernst reference cell has a high resistance at low temperatures (i.e. ambient temperatures) and a resistance of approximately 80-100 ohms at normal operating temperature. So, by monitoring the internal resistance of the reference cell it is possible to determine an accurate UEGO probe temperature, without the need of an external temperature sensor element.
There are several methods available to measure the resistance of the reference cell, including disabling the pump circuit and applying a known constant current across the reference cell and measuring the resultant voltage, finally re-enabling the pump circuit. This method requires several analog switches to apply the current and re-establish the pump servo circuit when done. Also, if a bias is applied to the Nernst cell, then an opposite polarity current with the same duration needs to be applied in order to “reset” the polarization on the cell. The one problem with this method is that it is “intrusive” to the feedback loop of the Nernst/pump.
Another method is to apply a high-frequency waveform to the pump circuit and measure the resultant deviation in EMF. The reference cell’s resistance is determined by AC-coupling a square wave of known amplitude and frequency via a series resistance, and measuring the resultant AC waveform’s amplitude. This waveform is always present, and since it is at a high frequency with respect to the response of the Nernst/pump feedback loop, it essentially averages out. This is the method employed in the PWB.
Circuit operation is very simple. A known square-wave source of 5 volts peak-to-peak and at a frequency of 1 to 3 KHz (generated by the DSP) is capacitively coupled to the reference cell positive terminal. Overall current is limited by a series resistance (plus Ri internal resistance) to 500 microamps peak to peak, or ±250 microamps around the Vbias point (Vbias is set to 2.5 volts to allow for bi-polar pump operation) – this value meets the specification outlined in the Bosch LSU 4.2 data sheet. The alternating current signal generates a corresponding alternating voltage with value based on the internal resistance Ri. For example, if Ri = 100 ohms, then 500 microamps (P-P) multiplied by 100 ohms yields 50 millivolts p-p, or ±25 mv around the Vbias point. Actually, the series current limit resistance and Ri form a resistor divider circuit driven by a voltage potential.
To measure the voltage, a capacitor is used to block the DC offset (i.e. reference cell voltage) and pass the alternating signal. A gain stage is introduced and the voltage is fed into a A/D port on a processor. Note that this signal is an AC signal, so ADC sampling needs to correlate with the polarity of applied square wave signal – this is known as synchronous rectification. An alternative method would be to use a bridge rectifier circuit to recover the positive/negative swings and then filter before application to the ADC channel.
Leaded Fuel
Wideband oxygen sensors are designed for an operational life of 100,000 miles (160,000 kms) under normal operating conditions. Replacement is required only if the sensor has failed due to unusual operating conditions, physical damage, or contamination. For example, a blown head gasket might allow silicon to enter the exhaust and contaminate the sensor. Oil burned in the combustion chamber due to leaking valve guides or rings can allow phosphorus to enter the exhaust and contaminate the sensor.
Depending on the lead contents of the used fuel, the expected service life time is:
- for 0.6 g Pb/l: 20,000 km (12,000 miles)
- for 0.4 g Pb/l: 30,000 km (18,000 miles)
- for 0.15 g Pb/l: 60,000 km (36,000 miles)
In general, when using leaded fuel, the sensor will need to be replaced when functional problems occur, e.g. instable idle speed, driveability problems. The following tests can be done for a rough check of the sensor function:
- Reasonableness of the signal check in rich exhaust gas: sensor signal should indicate rich
- Reasonableness of the signal check in “free-air”: sensor signal should indicate very air lean
- Heater cold resistance at room temperature, with a multimeter between grey and white cable (H+, H-), and the sensor not connected to the Precision Wideband Controller, should be 2.5 to less than 10 ohms
* We dedicate the Precision Wideband Controller to the memory of Garfield Willis. Garfield was instrumental in early research and development of the EGOR wideband controller.
Last Updated: 05/04/2020 09:45:16
MegaSquirt® and MicroSquirt® controllers are experimental devices intended for educational purposes.
MegaSquirt® and MicroSquirt® controllers are not for sale or use on pollution controlled vehicles. Check the laws that apply in your locality to determine if using a MegaSquirt® or MicroSquirt® controller is legal for your application.
©2004, 2007 Bruce Bowling and Al Grippo and Lance Gardiner. All rights reserved. MegaSquirt® and MicroSquirt® are registered trademarks. This document is solely for the support of MegaSquirt® boards from Bowling and Grippo.